Binary Tree - 理論篇
#clippings
dfs: 先往深走,遇到葉子節點再往回走。
bfs: 一層一層遍歷。
- dfs
- 前序遍歷(遞歸法,迭代法)
- 中序遍歷(遞歸法,迭代法)
- 後序遍歷(遞歸法,迭代法)
- bfs
- 層次遍歷(迭代法)
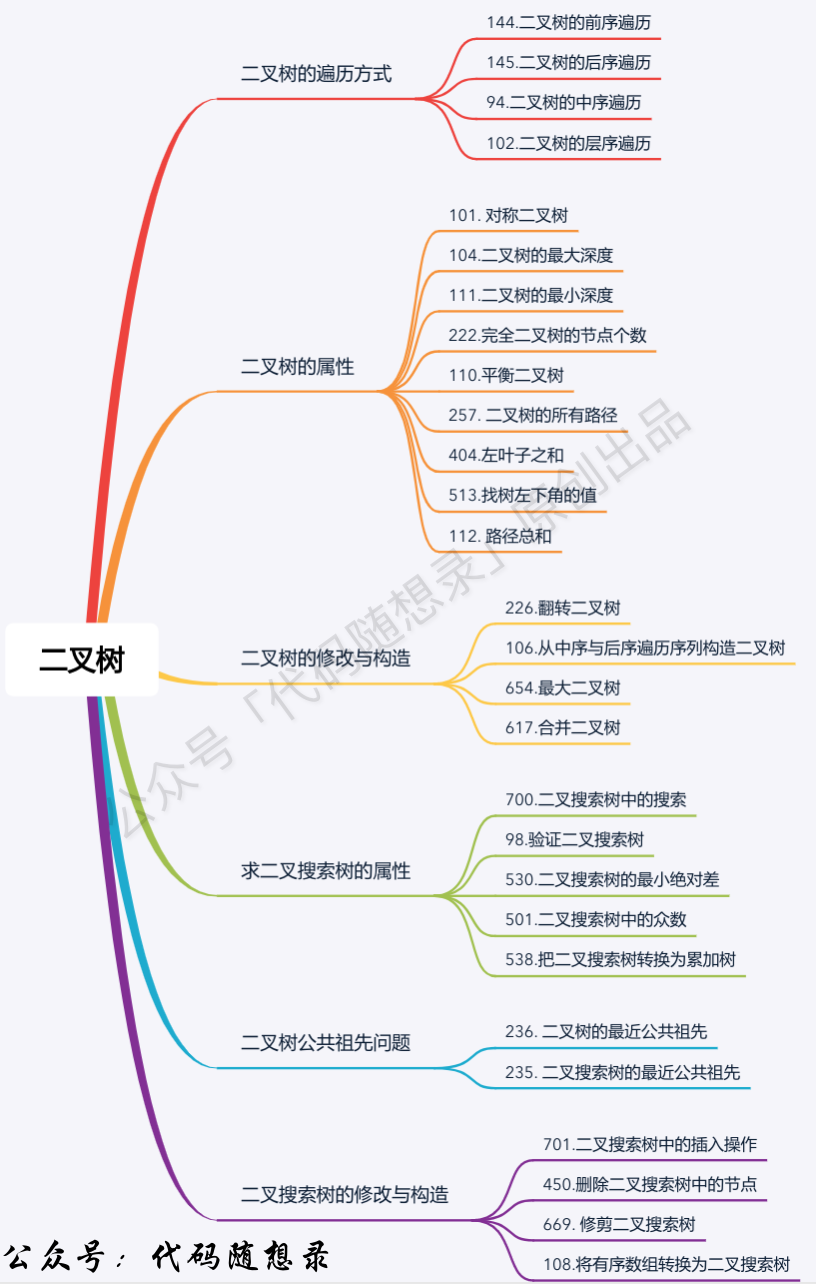
說到二叉樹,大家對於二叉樹其實都很熟悉了,本文呢我也不想教科書式的把二叉樹的基礎內容再囉嗦一遍,所以以下我講的都是一些比較重點的內容。
相信只要耐心看完,都會有所收穫。
二叉樹的種類
在我們解題過程中二叉樹有兩種主要的形式:滿二叉樹和完全二叉樹。
滿二叉樹
滿二叉樹:如果一棵二叉樹只有度為0的結點和度為2的結點,並且度為0的結點在同一層上,則這棵二叉樹為滿二叉樹。
如圖所示:
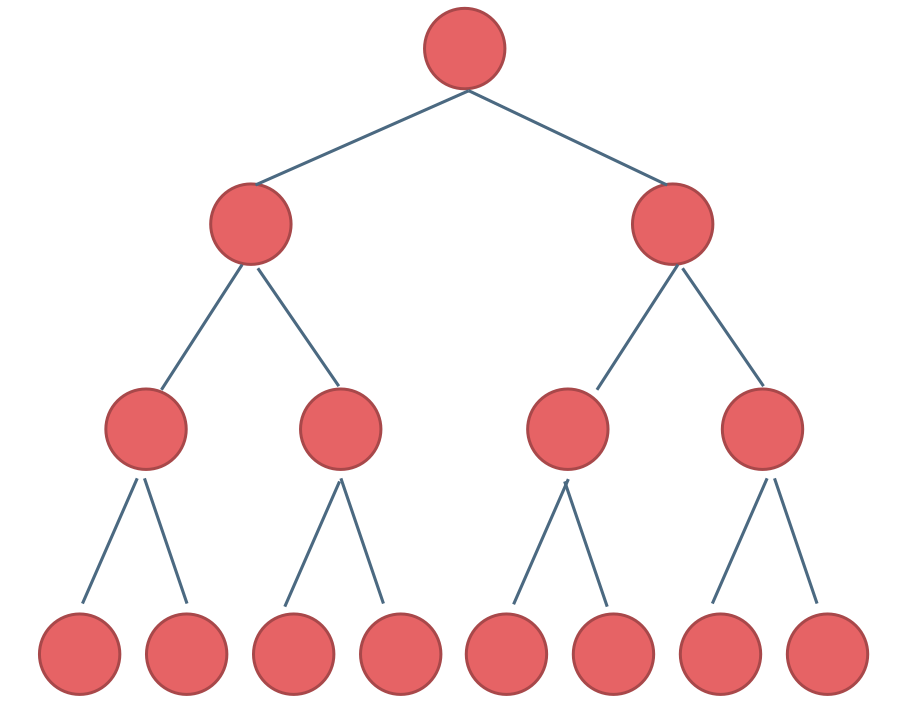
這棵二叉樹為滿二叉樹,也可以說深度為k,有2^k-1個節點的二叉樹。
完全二叉樹
什麼是完全二叉樹?
完全二叉樹的定義如下:在完全二叉樹中,除了最底層節點可能沒填滿外,其餘每層節點數都達到最大值,並且最下面一層的節點都集中在該層最左邊的若干位置。若最底層為第 h 層,則該層包含 1~ 2^(h-1) 個節點。
大家要自己看完全二叉樹的定義,很多同學對完全二叉樹其實不是真正的懂了。
我來舉一個典型的例子如題:
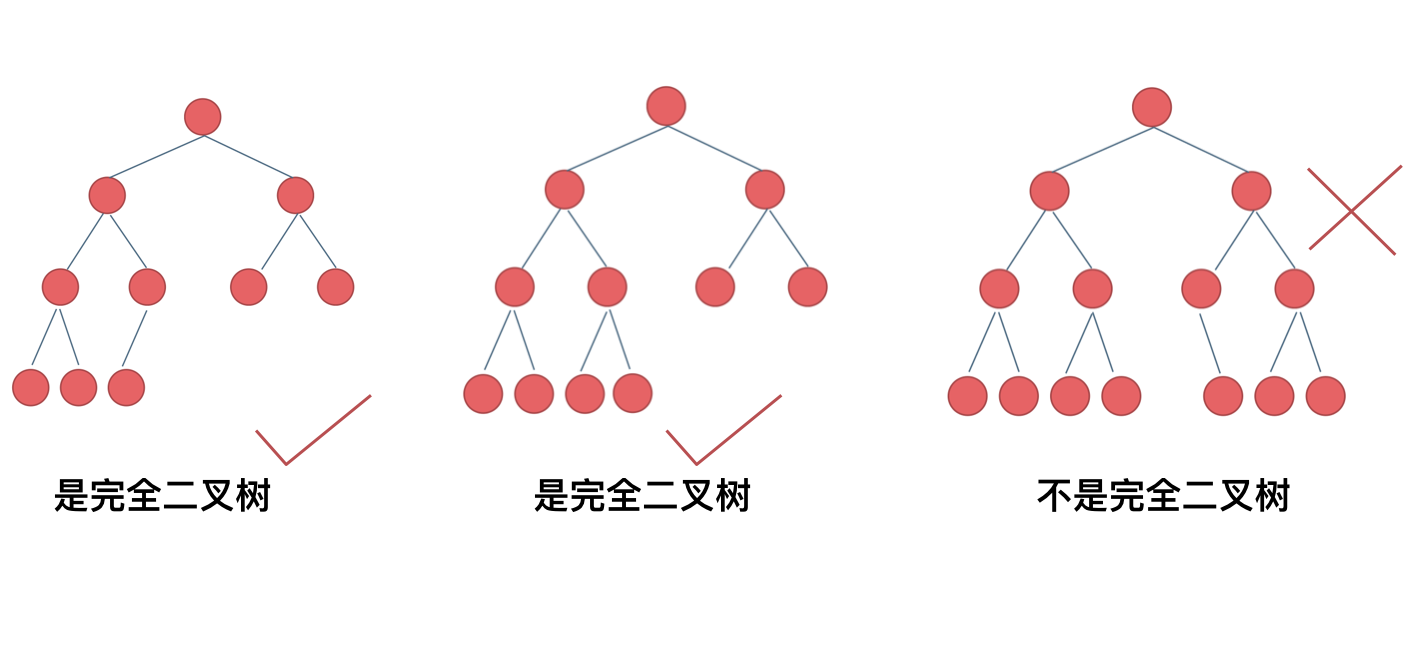
相信不少同學最後一個二叉樹是不是完全二叉樹都中招了。
之前我們剛剛講過優先級隊列其實是一個堆,堆就是一棵完全二叉樹,同時保證父子節點的順序關係。
二叉搜索樹
前面介紹的樹,都沒有數值的,而二叉搜索樹是有數值的了, 二叉搜索樹是一個有序樹。
- 若它的左子樹不空,則左子樹上所有結點的值均小於它的根結點的值;
- 若它的右子樹不空,則右子樹上所有結點的值均大於它的根結點的值;
- 它的左、右子樹也分別為二叉排序樹
下面這兩棵樹都是搜索樹 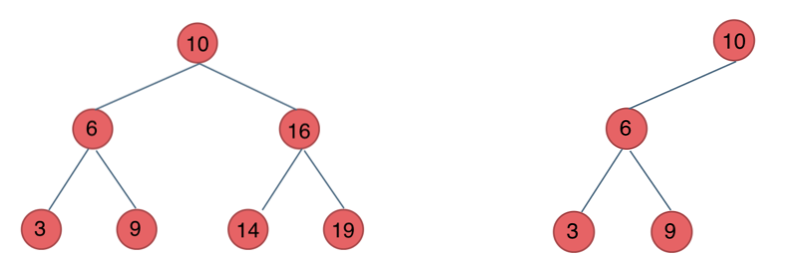
平衡二叉搜索樹
平衡二叉搜索樹:又被稱為AVL(Adelson-Velsky and Landis)樹,且具有以下性質:它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1,並且左右兩個子樹都是一棵平衡二叉樹。
如圖:
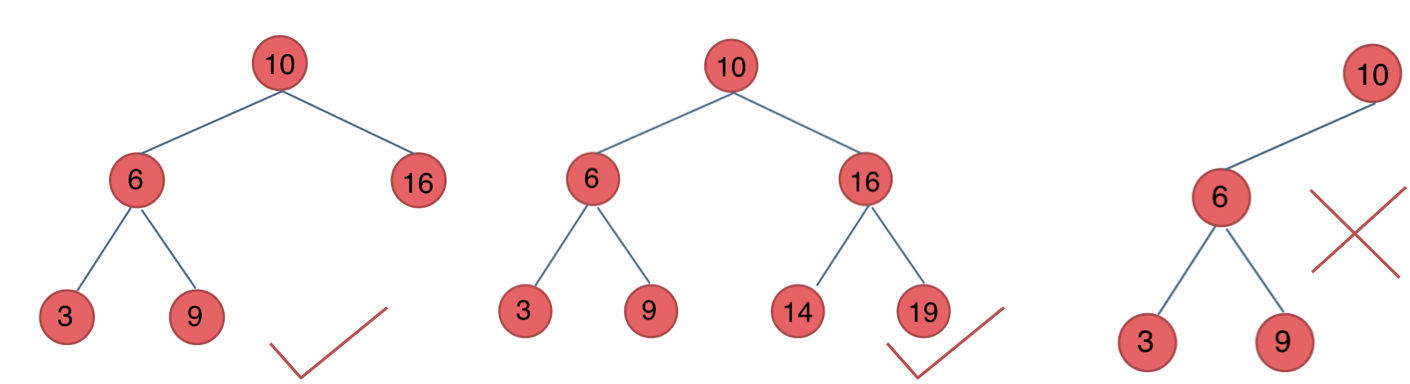
最後一棵 不是平衡二叉樹,因為它的左右兩個子樹的高度差的絕對值超過了1。
C++中map、set、multimap,multiset的底層實現都是平衡二叉搜索樹,所以map、set的增刪操作時間時間複雜度是logn,注意我這裡沒有說unordered_map、unordered_set,unordered_map、unordered_set底層實現是哈希表。
所以大家使用自己熟悉的編程語言寫算法,一定要知道常用的容器底層都是如何實現的,最基本的就是map、set等等,否則自己寫的代碼,自己對其性能分析都分析不清楚!
二叉樹的存儲方式
二叉樹可以鏈式存儲,也可以順序存儲。
那麼鏈式存儲方式就用指針, 順序存儲的方式就是用數組。
顧名思義就是順序存儲的元素在內存是連續分佈的,而鏈式存儲則是通過指針把分佈在各個地址的節點串聯一起。
鏈式存儲如圖:
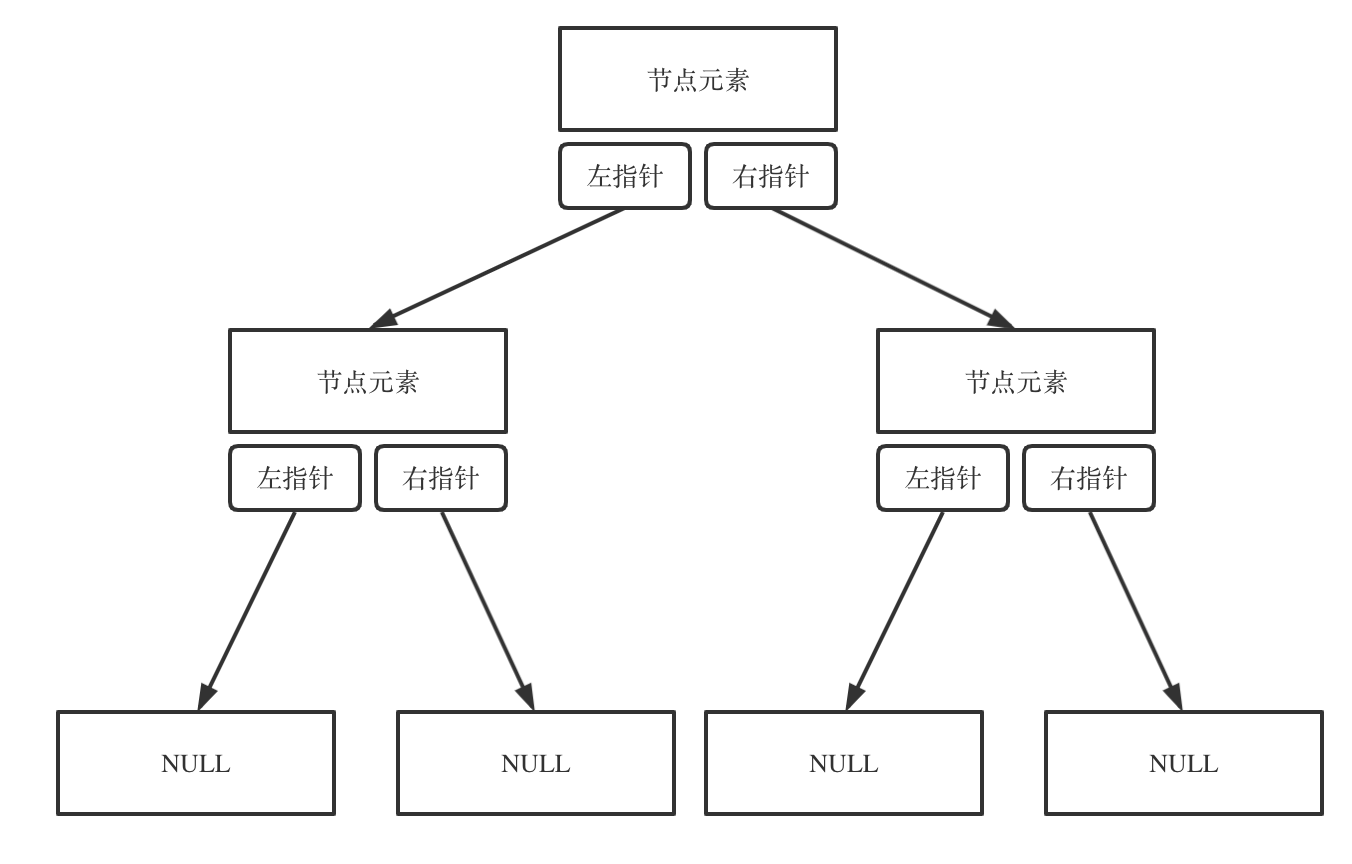
鏈式存儲是大家很熟悉的一種方式,那麼我們來看看如何順序存儲呢?
其實就是用數組來存儲二叉樹,順序存儲的方式如圖:
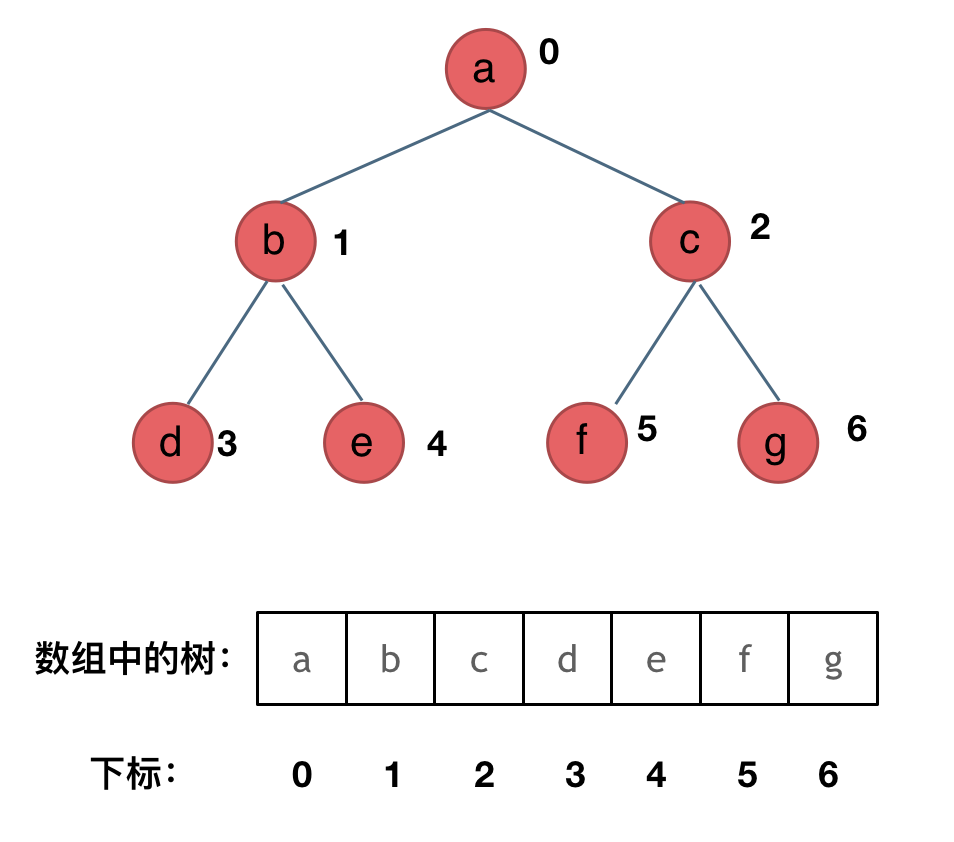
用數組來存儲二叉樹如何遍歷的呢?
**如果父節點的數組下標是 i,那麼它的左孩子就是 i \* 2 + 1,右孩子就是 i \* 2 + 2。**但是用鏈式表示的二叉樹,更有利於我們理解,所以一般我們都是用鏈式存儲二叉樹。
所以大家要瞭解,用數組依然可以表示二叉樹。
二叉樹的遍歷方式
關於二叉樹的遍歷方式,要知道二叉樹遍歷的基本方式都有哪些。
一些同學用做了很多二叉樹的題目了,可能知道前中後序遍歷,可能知道層序遍歷,但是卻沒有框架。
我這裡把二叉樹的幾種遍歷方式列出來,大家就可以一一串起來了。
二叉樹主要有兩種遍歷方式:
- 深度優先遍歷:先往深走,遇到葉子節點再往回走。
- 廣度優先遍歷:一層一層的去遍歷。
這兩種遍歷是圖論中最基本的兩種遍歷方式,後面在介紹圖論的時候 還會介紹到。
那麼從深度優先遍歷和廣度優先遍歷進一步拓展,才有如下遍歷方式:
- 深度優先遍歷 (DFS)
- 前序遍歷(遞歸法,迭代法)
- 中序遍歷(遞歸法,迭代法)
- 後序遍歷(遞歸法,迭代法)
- 廣度優先遍歷 (BFS)
- 層次遍歷(迭代法)
在深度優先遍歷中:有三個順序,前中後序遍歷, 有同學總分不清這三個順序,經常搞混,我這裡教大家一個技巧。
這裡前中後,其實指的就是中間節點的遍歷順序,只要大家記住 前中後序指的就是中間節點的位置就可以了。
看如下中間節點的順序,就可以發現,中間節點的順序就是所謂的遍歷方式
- 前序遍歷:中左右
- 中序遍歷:左中右
- 後序遍歷:左右中
大家可以對著如下圖,看看自己理解的前後中序有沒有問題。
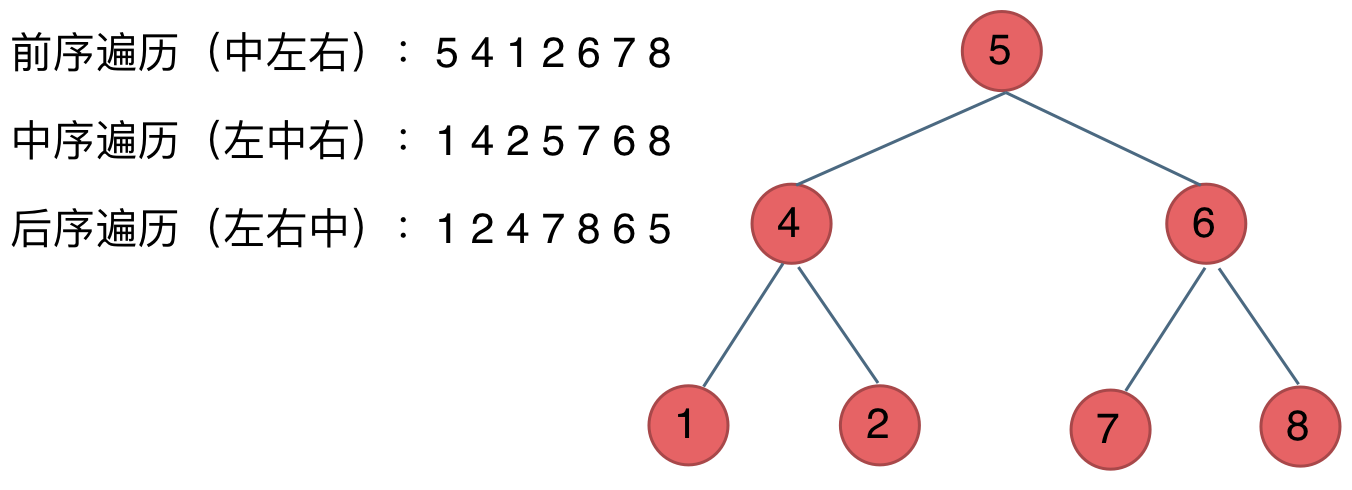
最後再說一說二叉樹中深度優先和廣度優先遍歷實現方式,我們做二叉樹相關題目,經常會使用遞歸的方式來實現深度優先遍歷,也就是實現前中後序遍歷,使用遞歸是比較方便的。
**之前我們講棧與隊列的時候,就說過棧其實就是遞歸的一種實現結構**,也就說前中後序遍歷的邏輯其實都是可以借助棧使用非遞歸的方式來實現的。而廣度優先遍歷的實現一般使用隊列來實現,這也是隊列先進先出的特點所決定的,因為需要先進先出的結構,才能一層一層的來遍歷二叉樹。
這裡其實我們又瞭解了棧與隊列的一個應用場景了。
具體的實現我們後面都會講的,這裡大家先要清楚這些理論基礎。
二叉樹的定義
剛剛我們說過了二叉樹有兩種存儲方式順序存儲,和鏈式存儲,順序存儲就是用數組來存,這個定義沒啥可說的,我們來看看鏈式存儲的二叉樹節點的定義方式。
C++代碼如下:
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
大家會發現二叉樹的定義 和鏈表是差不多的,相對於鏈表 ,二叉樹的節點裡多了一個指針, 有兩個指針,指向左右孩子。
這裡要提醒大家要注意二叉樹節點定義的書寫方式。
在現場面試的時候 面試官可能要求手寫代碼,所以數據結構的定義以及簡單邏輯的代碼一定要鍛鍊白紙寫出來。
因為我們在刷leetcode的時候,節點的定義默認都定義好了,真到面試的時候,需要自己寫節點定義的時候,有時候會一臉懵逼!
總結
二叉樹是一種基礎數據結構,在算法面試中都是常客,也是眾多數據結構的基石。
本篇我們介紹了二叉樹的種類、存儲方式、遍歷方式以及定義,比較全面的介紹了二叉樹各個方面的重點,幫助大家掃一遍基礎。
說到二叉樹,就不得不說遞歸,很多同學對遞歸都是又熟悉又陌生,遞歸的代碼一般很簡短,但每次都是一看就會,一寫就廢。