空間複雜度分析

source:: 空間複雜度分析 | 代碼隨想錄

#clippings

空間複雜度簡介

那麼一直還沒有講空間複雜度，所以打算陸續來補上，內容不難，大家可以讀一遍文章就有整體的瞭解了。

什麼是空間複雜度呢？

是對一個算法在運行過程中占用內存空間大小的量度，記做S(n)=O(f(n)。

空間複雜度(Space Complexity)記作S(n) 依然使用大O來表示。利用程序的空間複雜度，可以對程序運行中需要多少內存有個預先估計。

關注空間複雜度有兩個常見的相關問題

空間複雜度是考慮程序（可執行文件）的大小麼？

很多同學都會混淆程序運行時內存大小和程序本身的大小。這裡強調一下空間複雜度是考慮程序運行時占用內存的大小，而不是可執行文件的大小。

空間複雜度是準確算出程序運行時所占用的內存麼？

不要以為空間複雜度就已經精準的掌握了程序的內存使用大小，很多因素會影響程序真正內存使用大小，例如編譯器的內存對齊，編程語言容器的底層實現等等這些都會影響到程序內存的開銷。

所以空間複雜度是預先大體評估程序內存使用的大小。

說到空間複雜度，我想同學們在OJ（online judge）上應該遇到過這種錯誤，就是超出內存限制，一般OJ對程序運行時的所消耗的內存都有一個限制。

為了避免內存超出限制，這也需要我們對算法占用多大的內存有一個大體的預估。

同樣在工程實踐中，計算機的內存空間也不是無限的，需要工程師對軟件運行時所使用的內存有一個大體評估，這都需要用到算法空間複雜度的分析。

來看一下例子，什麼時候的空間複雜度是 $O(1)$ 呢，C++代碼如下：

int j = 0;
for (int i = 0; i < n; i++) {
    j++;
}

第一段代碼可以看出，隨著n的變化，所需開闢的內存空間並不會隨著n的變化而變化。即此算法空間複雜度為一個常量，所以表示為大O(1)。

什麼時候的空間複雜度是O(n)？

當消耗空間和輸入參數n保持線性增長，這樣的空間複雜度為O(n)，來看一下這段C++代碼

int * a = new int(n);
for (int i = 0; i < n; i++) {
    a[i] = i;
}

我們定義了一個數組出來，這個數組占用的大小為n，雖然有一個for循環，但沒有再分配新的空間，因此，這段代碼的空間複雜度主要看第一行即可，隨著n的增大，開闢的內存大小呈線性增長，即 O(n)。

其他的 O(n^2)， O(n^3) 我想大家應該都可以以此例舉出來了，那麼思考一下什麼時候空間複雜度是 O(logn)呢？

空間複雜度是logn的情況確實有些特殊，其實是在遞歸的時候，會出現空間複雜度為logn的情況。

本篇講通過求斐波那契數列和二分法再來深入分析一波遞歸算法的時間和空間複雜度，細心看完，會刷新對遞歸的認知！

遞歸求斐波那契數列的性能分析

先來看一下求斐波那契數的遞歸寫法。

int fibonacci(int i) {
       if(i <= 0) return 0;
       if(i == 1) return 1;
       return fibonacci(i-1) + fibonacci(i-2);
}

對於遞歸算法來說，代碼一般都比較簡短，從算法邏輯上看，所用的存儲空間也非常少，但運行時需要內存可不見得會少。

時間複雜度分析

來看看這個求斐波那契的遞歸算法的時間複雜度是多少呢？

在講解遞歸時間複雜度的時候，我們提到了遞歸算法的時間複雜度本質上是要看: ==遞歸的次數 * 每次遞歸的時間複雜度==。

可以看出上面的代碼每次遞歸都是O(1)的操作。再來看遞歸了多少次，這裡將i為5作為輸入的遞歸過程抽象成一棵遞歸樹，如圖：

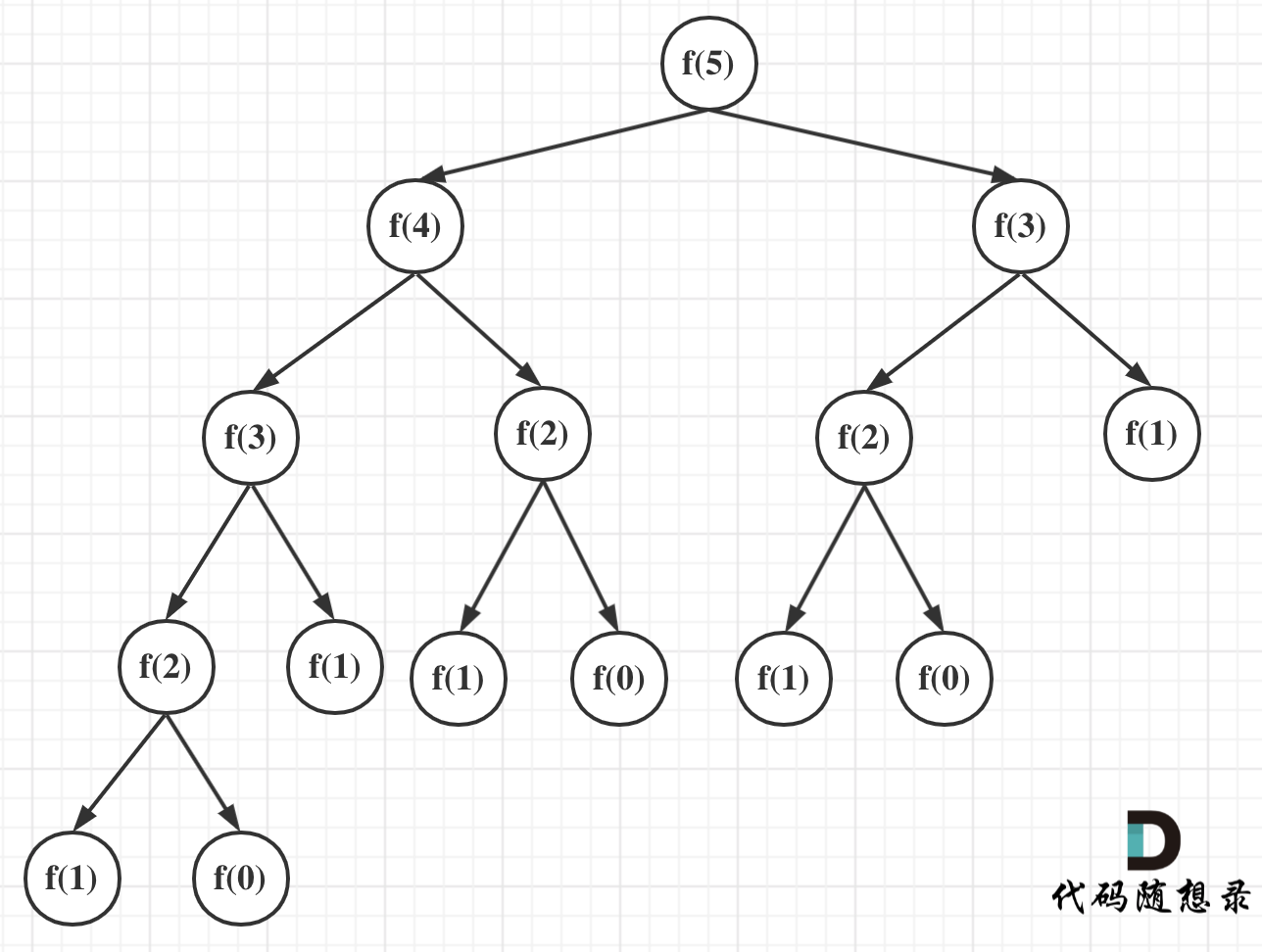
遞歸空間複雜度分析

從圖中，可以看出f(5)是由f(4)和f(3)相加而來，那麼f(4)是由f(3)和f(2)相加而來以此類推。

在這棵二叉樹中每一個節點都是一次遞歸，那麼這棵樹有多少個節點呢？

我們之前也有說到，一棵深度（按根節點深度為1）為k的二叉樹最多可以有 2^k - 1 個節點。

所以該遞歸算法的時間複雜度為O(2^n)，這個複雜度是非常大的，隨著n的增大，耗時是指數上升的。

來做一個實驗，大家可以有一個直觀的感受。

以下為C++代碼，來測一下，讓我們輸入n的時候，這段遞歸求斐波那契代碼的耗時。

#include <iostream>
#include <chrono>
#include <thread>
using namespace std;
using namespace chrono;
int fibonacci(int i) {
       if(i <= 0) return 0;
       if(i == 1) return 1;
       return fibonacci(i - 1) + fibonacci(i - 2);
}
void time_consumption() {
    int n;
    while (cin >> n) {
        milliseconds start_time = duration_cast<milliseconds >(
            system_clock::now().time_since_epoch()
        );

        fibonacci(n);

        milliseconds end_time = duration_cast<milliseconds >(
            system_clock::now().time_since_epoch()
        );
        cout << milliseconds(end_time).count() - milliseconds(start_time).count()
            <<" ms"<< endl;
    }
}
int main()
{
    time_consumption();
    return 0;
}

根據以上代碼，給出幾組實驗數據：

測試電腦以2015版MacPro為例，CPU配置：2.7 GHz Dual-Core Intel Core i5

測試數據如下：

n = 40，耗時：837 ms
n = 50，耗時：110306 ms

可以看出，O(2^n)這種指數級別的複雜度是非常大的。

所以這種求斐波那契數的算法看似簡潔，其實時間複雜度非常高，一般不推薦這樣來實現斐波那契。

其實罪魁禍首就是這裡的兩次遞歸，導致了時間複雜度以指數上升。

return fibonacci(i-1) + fibonacci(i-2);

可不可以優化一下這個遞歸算法呢。主要是減少遞歸的調用次數。

來看一下如下代碼：

int fibonacci(int first, int second, int n) {
    if (n <= 0) {
        return 0;
    }
    if (n < 3) {
        return 1;
    }
    else if (n == 3) {
        return first + second;
    }
    else {
        return fibonacci(second, first + second, n - 1);
    }
}

這裡相當於用first和second來記錄當前相加的兩個數值，此時就不用兩次遞歸了。

因為每次遞歸的時候n減1，即只是遞歸了n次，所以時間複雜度是 O(n)。

同理遞歸的深度依然是n，每次遞歸所需的空間也是常數，所以空間複雜度依然是O(n)。

代碼（版本二）的複雜度如下：

時間複雜度：O(n)
空間複雜度：O(n)

此時再來測一下耗時情況驗證一下：

#include <iostream>
#include <chrono>
#include <thread>
using namespace std;
using namespace chrono;
int fibonacci_3(int first, int second, int n) {
    if (n <= 0) {
        return 0;
    }
    if (n < 3) {
        return 1;
    }
    else if (n == 3) {
        return first + second;
    }
    else {
        return fibonacci_3(second, first + second, n - 1);
    }
}

void time_consumption() {
    int n;
    while (cin >> n) {
        milliseconds start_time = duration_cast<milliseconds >(
            system_clock::now().time_since_epoch()
        );

        fibonacci_3(1, 1, n);

        milliseconds end_time = duration_cast<milliseconds >(
            system_clock::now().time_since_epoch()
        );
        cout << milliseconds(end_time).count() - milliseconds(start_time).count()
            <<" ms"<< endl;
    }
}
int main()
{
    time_consumption();
    return 0;
}

測試數據如下：

n = 40，耗時：0 ms
n = 50，耗時：0 ms

大家此時應該可以看出差距了！！

空間複雜度分析

說完了這段遞歸代碼的時間複雜度，再看看如何求其空間複雜度呢，這裡給大家提供一個公式：==遞歸算法的空間複雜度 = 每次遞歸的空間複雜度 * 遞歸深度==

為什麼要求遞歸的深度呢？

因為每次遞歸所需的空間都被壓到調用棧裡（這是內存管理裡面的數據結構，和算法裡的棧原理是一樣的），一次遞歸結束，這個棧就是就是把本次遞歸的數據彈出去。所以這個棧最大的長度就是遞歸的深度。

此時可以分析這段遞歸的空間複雜度，從代碼中可以看出每次遞歸所需要的空間大小都是一樣的，所以每次遞歸中需要的空間是一個常量，並不會隨著n的變化而變化，每次遞歸的空間複雜度就是 $O(1)$ 。

在看遞歸的深度是多少呢？如圖所示：

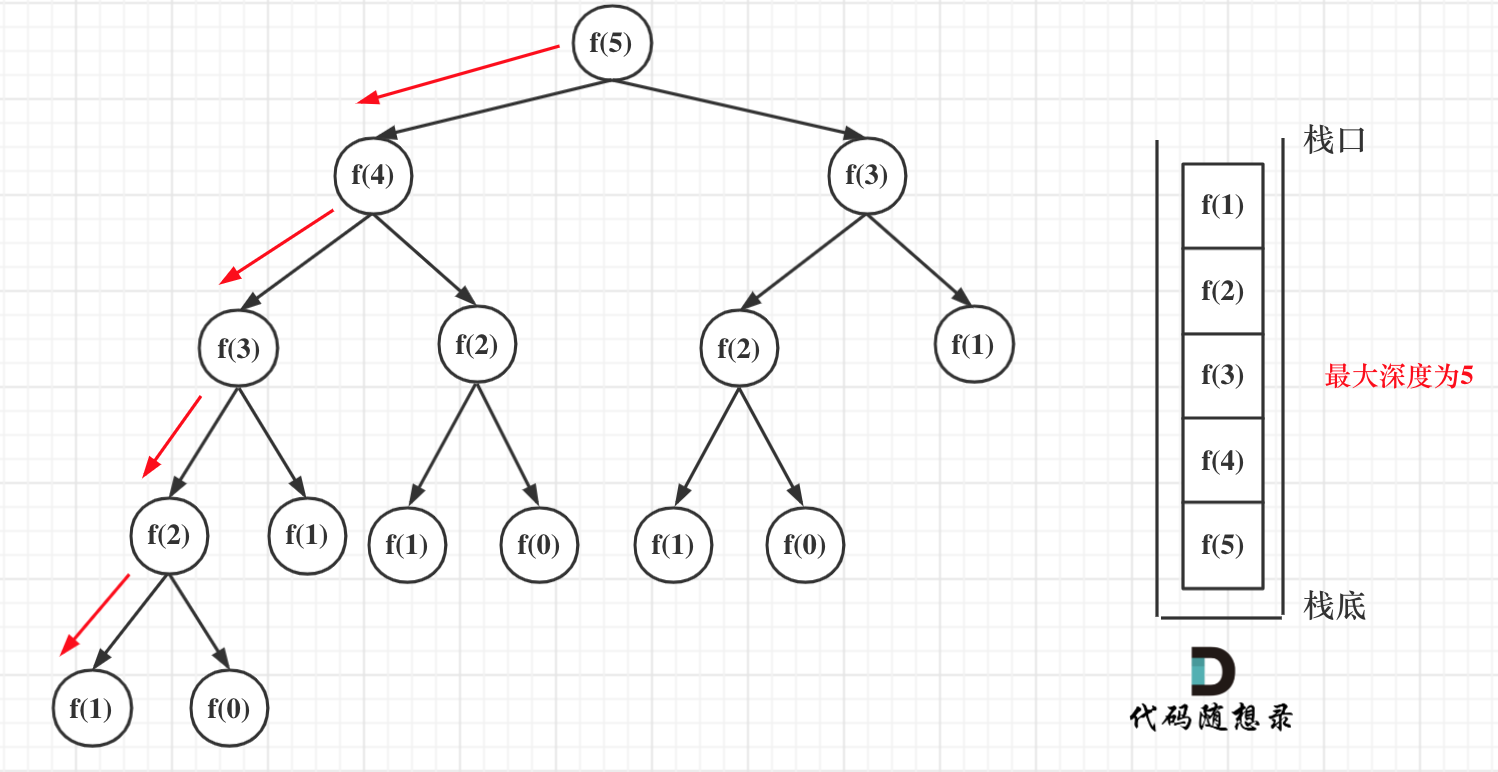
遞歸空間複雜度分析

遞歸第n個斐波那契數的話，遞歸調用棧的深度就是n。

那麼每次遞歸的空間複雜度是O(1)，調用棧深度為n，所以這段遞歸代碼的空間複雜度就是O(n)。

int fibonacci(int i) {
       if(i <= 0) return 0;
       if(i == 1) return 1;
       return fibonacci(i-1) + fibonacci(i-2);
}

最後對各種求斐波那契數列方法的性能做一下分析，如題：

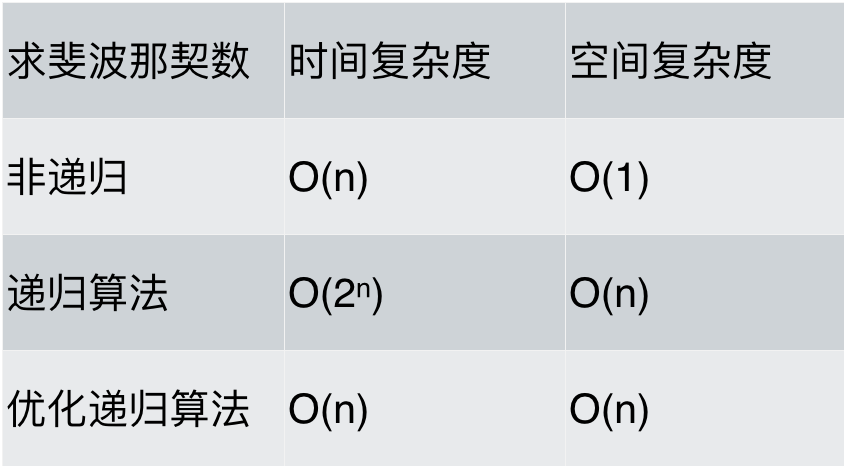
遞歸的空間複雜度分析

可以看出，求斐波那契數的時候，使用遞歸算法並不一定是在性能上是最優的，但遞歸確實簡化的代碼層面的複雜度。

二分法（遞歸實現）的性能分析

帶大家再分析一段二分查找的遞歸實現。

int binary_search( int arr[], int l, int r, int x) {
    if (r >= l) {
        int mid = l + (r - l) / 2;
        if (arr[mid] == x)
            return mid;
        if (arr[mid] > x)
            return binary_search(arr, l, mid - 1, x);
        return binary_search(arr, mid + 1, r, x);
    }
    return -1;
}

都知道二分查找的時間複雜度是O(logn)，那麼遞歸二分查找的空間複雜度是多少呢？

我們依然看 每次遞歸的空間複雜度和遞歸的深度

每次遞歸的空間複雜度可以看出主要就是參數里傳入的這個arr數組，但需要注意的是在C/C++中函數傳遞數組參數，不是整個數組拷貝一份傳入函數而是傳入的數組首元素地址。

也就是說每一層遞歸都是公用一塊數組地址空間的，所以每次遞歸的空間複雜度是常數即：O(1)。

再來看遞歸的深度，二分查找的遞歸深度是logn ，遞歸深度就是調用棧的長度，那麼這段代碼的空間複雜度為 1 * logn = O(logn)。

大家要注意自己所用的語言在傳遞函數參數的時，是拷貝整個數值還是拷貝地址，如果是拷貝整個數值那麼該二分法的空間複雜度就是O(nlogn)。

總結

本章我們詳細分析了遞歸實現的求斐波那契和二分法的空間複雜度，同時也對時間複雜度做了分析。

特別是兩種遞歸實現的求斐波那契數列，其時間複雜度截然不容，我們還做了實驗，驗證了時間複雜度為O(2^n)是非常耗時的。

通過本篇大家應該對遞歸算法的時間複雜度和空間複雜度有更加深刻的理解了。